近期阅读 UCL Johannes Heinrich 和 David Silver 关于博弈的均衡求解论文,我发现他们给出的方法实际上是一种比较强大且通用的技术,有必要深入研究一下。对这篇文章的解读,不得不提的是他们和在 2015 年的前篇。在那里对基础内容似乎讲解的更加详细。然而,由于其工作的交叉领域中各自的术语差异较大,所以在理解论文时会造成一定的麻烦,本文期望从 NSFP 出发完整地分析涉及到的相关领域中的问题,结合算法谈谈如何使用这项新的技术来解决若干领域中的有趣问题。
前期是为了理解所以大部分内容是直接翻译该论文的工作。计划在今后细化讲解,争取把这一套方法完整地展示清楚。
NFSP 就是引入神经网络近似函数的 FSP,是一种利用强化学习技术来从自我博弈中学习近似纳什均衡的方法。解决了三个问题:
- 无先验知识 NFSP agent 学习
- 运行时不依赖局部搜索
- 收敛到自我对局的近似纳什均衡
这是一般的不完美信息二人零和博弈。虚拟对弈同样也会收敛到合作、势力场博弈的纳什均衡。所以 NFSP 也能够成功应用在这些博弈上。另外,近期的研究关于连续空间行动的强化学习(Lillicrap et al. 2015)也能够应用在连续行动博弈中,目前的博弈论方法并不能直接处理这样的情形。
然而我们需要知道了解相关的基础,才能够真切地了解这篇文章给我们带来了什么启发。本文在对原文理解基础上进行翻译,后续会继续增加向前的回溯和向后的扩展。
强化学习
首先是强化学习基础。强化学习中的 agent 需要学会通过和环境交互中最大化自己的期望未来回报。一般来说,环境会被建模为一个 MDP。
很多强化学习算法从序列化经验中学习。这些经验的形如 $(s_t, a_t, r_{t+1},s_{t+1})$,其中的 $s_t$ 是在时间 $t$ 的状态,$a_t$ 是在那个状态下选择的行动,$r_{t+1}$ 是之后的回报,$s_{t+1}$ 是转移的下一个状态。常见的目标函数是学习 行动-值函数,$Q(s,a) = \mathbb{E}^{\pi}[G_{t} | S_{t} =s, A_{t} = a]$,定义为在状态 $s$ 采取行动 $a$ 并采取策略 $\pi$ 的期望收益。
同策略(on-policy)学习是指 agent 学习当前采用的策略。异策略(off-policy)学习则是 agent 从另一个 agent 或者另一个策略(如之前的策略)的经验中学习。
Q-learning 是一种异策略学习方法。其学习的是贪婪策略——在每个状态下,都会选择有最高的估计值的行动。通过应用异策略强化学习方法在 respective 转移元组来存储和回放过去的经验的方法称为经验回放。Fitted Q Iteration (FQI)是一种采用经验回放的 Q-learning 的批量强化学习方法。Neural Fitted Q Iteration(NFQ)和 Deep Q Network(DQN)则分别是在批量和在线更新的 FQI 两种扩展。
展开式博弈
这是一类包含多个参与人的序列化交互的模型。参与人的目标是最大化自身的收益(payoff)。在不完美信息博弈中,每个参与人只会观察到自身的信息状态(information state),例如,在扑克游戏中,玩家只会知道自己私有的牌,并不知道其他人的。每个参与人会选择行为策略(behaviourial strategy)将信息状态映射到可选的行动的概率分布上。我们假设博弈是有完美回忆(perfect recall)的,每个参与人当前信息状态 $s_{t}^i$ 暗含了他自己的导致达到当前状态的信息状态和行动序列,$s_{1}^{i},a_{1}^{i},s_{2}^{i},a_{2}^{i},\dots,s_{t}^{i}$。realisation-probability,$x_{\pi^i}(s_{t}^i) = \prod_{k=1}^{t-1} \pi^i(s_{k}^{i}, a_{k}^{i})$,给出了参与人 $i$ 行为策略 $\pi^i$ 对实现他信息状态的 $s_{t}^i$ 的概率。策略组合(strategy profile)$\pi = (\pi^1,…,\pi^n)$ 是对所有参与人策略的集合。$\pi^{-i}$ 则是除去 $\pi^i$ 之外的 $\pi$ 中的策略。给定一个固定的策略组合 $\pi^{-i}$,参与人 $i$ 在这个设置下任何达到最优的收益都是一个最优反应(best response)。近似反应或者 $\epsilon$-最优反应是不超过 $\epsilon$ 的亚最优。纳什均衡是一个策略组合,其中每个参与人的策略都是对其他策略的最优策略。而近似纳什均衡或者 $\epsilon$-纳什均衡就是 $\epsilon$-最优反应的策略组合。由于在纳什均衡中没有参与人可以通过策略的偏移来提升自己的收益。所以,纳什均衡可以被当成理性自我对局学习的不动点。实际上,纳什均衡是唯一个理性 agent 在自我对局中可以收敛的策略组合。
虚拟自我对局 Fictitious Self Play, FSP
虚拟对局是从自我对局中学习的博弈论模型。自我对局的参与人选择针对其对手的平均行为的最佳反应。自我对局参与人的平均策略在某些类型的博弈(如二人零和博弈和多人势力场博弈)中都会收敛到纳什均衡。Leslie 和 Collins 在 2006 年给出了推广的弱化自我对局。这种模型和通常的自我博弈有着类似的收敛保证,但是允许有近似最优反应和扰动的平均策略更新,也让这个扩展模型对机器学习尤其合适。
自我对局通常使用规范式博弈定义,这与扩展式博弈在有效性上存在指数级差距。Heinrich 等人在 2005 年引入了 Full-Width Extensive Form FSP(XSP),可以让自我对局参与人使用行为式,扩展式进行策略更新,得到了线性的时间和空间复杂性。这里一个关键的洞察是对规范式策略的凸组合,$\hat{\sigma} = \lambda_1 \hat{\pi}_1 + \lambda_2 \hat{\pi}_2$ ,我们可以达到一个实现等价的行为策略 $\sigma$,通过设置该值为成比例于对应的实现概率的凸组合,
$$\sigma(s,a)\propto \lambda_1 x_{\pi_1}(s) \pi_1(s,a) + \lambda_2 x_{\pi_2}(s) \pi_2(s,a)\; \forall s, a, \tag{1}$$
其中 $\lambda_1 x_{\pi_1}(s) + \lambda_2 x_{\pi_2}(s)$ 是在信息状态 $s$ 的策略的规范化常量。除了在行为策略下定义自我对局的 full-width 平均策略更新外,公式 (1) 给出了从这样的策略的凸组合中采样数据集的一种方法。Heinrich 等人在 2015 提出了 Fictitious Self Play (FSP)的基于采样和机器学习的算法来近似 XFP。FSP 分别用强化学习和监督学习来替换最优反应计算和平均策略更新。特别地,FSP agent 产生他们在自我对局中的经验转换的数据集。每个 agent 存放了自身的转移元组 $(s_t, a_t, r_{t+1},s_{t+1})$ 在记忆 $\mathcal{M}_{RL}$ 中 ,这个为强化学习设计。而 agent 自身的行为 $(s_t, a_t)$ 被存放在另一个分开的记忆 $\mathcal{M}_{SL}$ 中,这为监督学习设计。自我对局的采样通过 agent 的强化学习的记忆来近似用其他参与人的平均策略组合定义的 MDP 的数据。因此,通过强化学习的 MDP 的近似解会产生一个近似的最优反应。类似地,agent 的监督学习记忆近似了 agent 本身的平均策略,这可以通过监督式的分类方法学习。
神经网络虚拟自我对局
进行了多种扩展:神经网络函数近似,reservoir 采样,anticipatory 动态性和完全基于 agent 方法。NFSP agent 和博弈中的其他参与人进行交互,并记住自身关于博弈状态转移的经验和自身的行为。NFSP 将这些记忆分成两个数据集——一个给深度强化学习,一个给监督学习使用。特别地,这个 agent 从 $\mathcal{M}_{RL}$ 的数据中使用异策略强化学习训练一个神经网络 $F_{Q}$ 来预测行为值,$Q(s,a)$。得到的网络定义了 agent 的近似最优策略 $\beta = \epsilon\mbox{-}\mathrm{greedy}(F_Q)$,这里根据概率 $\epsilon$ 选择随机行动,根据概率 $1- \epsilon$ 选最大化预测行为值的行动。NFSP agent 训练了另外一个神经网络,$F_{S}$ 在 $\mathcal{M}_{SL}$ 的数据中使用监督学习来模拟自己过去的行为。这个网络将状态映射到了行动概率上,定义了 agent 的平均策略,$\pi = F_{S}$。在博弈进行过程中,agent 从两个策略 $\beta$ 和 $\pi$ 的混合中选择策略。
尽管虚拟参与人通常是针对对手的平均策略进行最优反应,但在连续时间的动态虚拟对局参与人是对对手平均规范式策略 $\hat{\pi}_t^{-i} + \eta \frac{d}{d t} \hat{\pi}_t ^{-i}$ 短期预测的最优反应。研究表明,选择合适的,博弈相关的 $\eta$ 可以提高在均衡处的自我对局的稳定性。NFSP 使用 $\hat{\beta}_{t+1}^{i}- \hat{\pi}_t^{i} \approx \frac{d}{d t} \hat{\pi}_t^{i}$ 作为用在 anticipatory 动态中的离散时间导数近似值。注意 $\Delta \hat{\pi}_t^{i} \propto \hat{\beta}_{t+1}^{i} - \hat{\pi}_t ^{i}$ 是常见的离散时间自我对局的规范化更新方向。为了让一个 NFSP agent 计算近似对对手预测平均策略组合 $\sigma^{-i} \equiv \hat{\pi}^{-i} + \eta(\hat{\beta}^{-i} - \hat{\pi}^{-i})$ 的最优反应,$\beta^{i}$,agent 需要迭代求值并最大化其行动值,$Q^i(s,a) \approx \mathbb{E}_{\beta^{i},\sigma^{-i}} [G_t ^{i}|S_t =s, A_t =a]$。这个可以使用异策略强化学习,如 Q-learning 或者 DQN 在和对手的预测策略,$\sigma^{-i}$ 对局的经验上获得。为了确保 agent 的强化学习记忆,$\mathcal{M}_{RL}$ ,包含这种类型的经验,NFSP 需要所有的 agent 从 $\sigma \equiv (1 - \eta)\hat{\pi} + \eta (\hat{\beta})$ 选择他们的行动,其中 $\eta \in \mathbb{R}$ 被称为预测参数(anticipatory parameter)。
虚拟自我对局通常要保留平均规范式博弈的最优反应策略,$\hat{\pi}_T^{i} = \frac{1}{T} \sum_{t=1}^T \beta_t^{i}$。Heinrich 等人在 2015 年给出了使用采样和机器学习技术来产生数据并学习用展开式博弈形式表示的规范式博弈策略凸组合。例如,我们可以通过使用 $\beta_t^{i},\;t = 1,\dots,T$ 按照 $\frac{1}{T}$ 的比例来采样整个博弈的过程来产生展开式数据。NFSP 使用蓄水池采样(reservoir sampling)来记忆其平均最优反应的经验。agent 的监督式学习记忆,$\mathcal{M}_{SL}$ 是一个蓄水池仅仅会在采用其近似最优策略 $\beta$ 时增加经验。NFSP agent 通常会训练自己的平均策略网络 $\pi = F_S$ 来匹配其存储在自身监督学习记忆中的平均行为,例如通过优化过去行为的对数概率来进行训练。算法 1 给出了 NFSP,其中使用 DQN 作为强化学习的方法。
算法 1:神经网络虚拟自我对局 NFSP 算法
输入:
- $\Gamma$ {博弈}
- $\mathcal{M}_{RL}$, $\mathcal{M}_{SL}$ {RL 和 SL 记忆}
- $F_{Q}$, $F_{S}$ {行动值网络和策略网络}
- $\beta = \epsilon\mbox{-}\mathrm{GREEDY}(\mathcal{M}_{RL})$ {最优反应策略}
- $\pi = F_{S}$ {平均策略}
- $\sigma$ {当前策略}
输出: $\pi$ 自我对弈中的纳什均衡近似
function $\mathrm{STEP()}$:
- $s_{t}, r_{t}, c_{t} \leftarrow \mathrm{OBSERVE}(\gamma)$
- $a_t \leftarrow \mathrm{THINK}(s_t, r_t, c_t)$
- $\mathrm{ACT}(\Gamma,a_t)$
end function
function $\mathrm{THINK}(s_t, r_t, c_t)$
- if $c_t = 0$ {episode terminated} then
$\sigma \leftarrow \mathrm{SAMPLEPOLICY}(\beta, \pi)$
end if - if $s_{t-1} \not= \mathrm{nil}$ then
$\tau_t \leftarrow (s_{t-1} ,a_{t-1},r_t,s_t,c_t)$
$\mathrm{UPDATERLMEMORY}(\mathcal{M}_{RL} , \tau_t)$
end if - $a_t \leftarrow \mathrm{SAMPLEACTION}(\sigma)$
- if $\sigma = \beta$ then
$\mathrm{UPDATESLMEMORY}(\mathcal{M}_{SL} , (s_t , a_t))$
end if - $s_{t−1}\leftarrow s_t$
- $a_{t−1} \leftarrow a_t$
- $\beta \leftarrow \mathrm{REINFORCEMENTLEARNING(\mathcal{M}_{RL})}$
- $\pi \leftarrow \mathrm{SUPERVISEDLEARNING}(\mathcal{M}_{SL})$
end function
function $\mathrm{REINFORCEMENTLEARNINIG}(\mathcal{M}_{RL})$
- $F_Q \leftarrow \mathrm{DQN}(\mathcal{M}_{RL})$
- return $\epsilon\mbox{-}\mathrm{GREEDY}(F_Q)$
end function
function $\mathrm{SUPERVISEDLEARNING}(\mathcal{M}_{SL})$
- $F_S \leftarrow$ 作用随机梯度下降到损失函数上:
$$\mathbb{E}_{(s,a)\sim \mathcal{M}_{SL}} [−\log\pi(s,a)]$$ - return $F_S$
end function
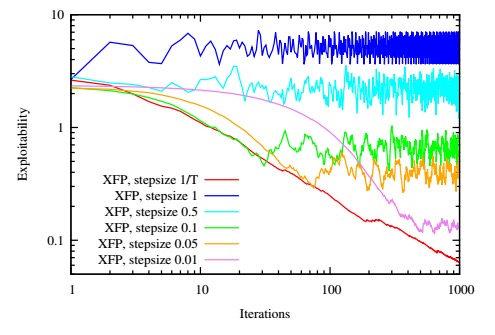
实验